All Sorts of Sorts

CSCI 362 - Data Structures

Prof. William Killian

Agenda

• Comparison-based sorting analysis
• Radix Sort
• Counting Sort

Sorting Overview/Wrap up

• Insertion Sort
  • Pros: easy, fast on small inputs, fast on nearly sorted
  • Cons: $O(N^2)$ worst, average, reverse-sorted
• Shell Sort
  • Pros: Easy to code, fast on nearly-sorted
  • Cons: $O(N^{1.5}$ worst case; perf sensitive to decrement sequence
• Heap Sort
  • Pros: $O(N~lg~N)$ worst case, sorts in place
  • Cons: moves a lot of elements around (make_heap, N * pop_heap)

Divide and Conquer Strategies

• Merge Sort
  • Pros: $O(N~lg~N)$ worst case
  • Cons: typically doesn't sort in place, shuffles elements around
• Quick Sort
  • Pros: $O(N~lg~N)$ average case, fast in practice
  • Cons: $O(N^2)$ worst case -- address this with median-of-3

How fast can we sort?

• Comparison-based sorts
• Theorem: all comparison sorts are $\Omega (N~lg~N)$
  • A comparison sort MUST perform $\Omega (N)$ comparisons

Decision Trees

Provide an Abstraction of comparison-based sorts

Key point: represent comparisons as edges on a tree. Nodes represent comparisons

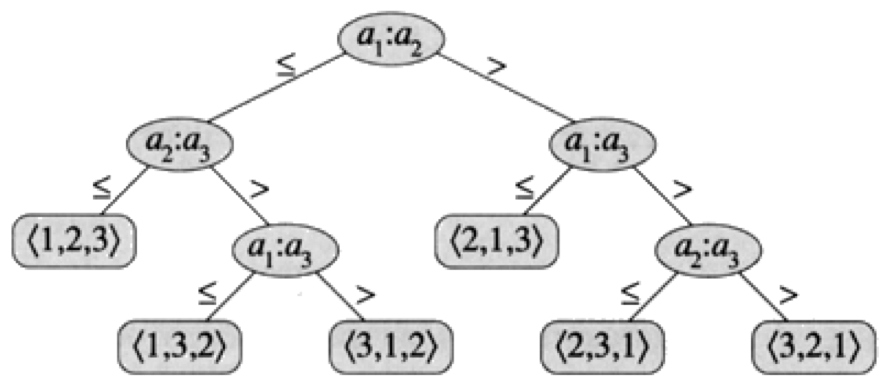
What is the asymptotic height of any decision tree for sorting $N$ elements?

A lower bound for comparison sorting

Theorem: Any decision tree that sorts $N$ elements has height $\Omega(N lg N)$

• What's the minimum number of leaves?
• What's the maximum number of leaves of a binary tree of height $h$?
• Clearly, min. number of leaves is <= max. number of leaves

Fun math!

• $N!$ possible permutations of all orderings for $N$ elements

$$N! \le 2^h$$

• Taking logarithms:

$$lg (N!) \le h$$

• Stirling's approximation tells us: $$ N! > {\left(\frac{N}{e}\right)}^N $$

Fun math! (continued)

• Thus we can claim the following:

  $$ h \ge lg {\left(\frac{N}{e}\right)}^N $$

• Rules of logarithms:

  $$ h \ge N~lg~N - N~lg~e$$

• Removing constants ($N~lg~e$)

  $$\Omega(N~lg~N)$$

Radix Sort

Idea: Don't compare the actual values. Instead, look at a single "digit" at a time

Example: $91, 06, 85, 15, 92, 35, 30, 22, 39$

int digit (int value, int place, int base = 10) {
    while (place--) {
        value /= base;
    }
    return value % base;
}

#include <vector>
using Bin = std::vector<int>;
Bin bins[10];

std::vector<int> data {91, 6, 85, 15, 92, 35, 30, 22, 39};

• 1). Start with 10 bins (base-10 number system representing 0-9 for digits)
• 2). Distribute all numbers from data into bins according to the one's digit (Least Significant Digit)

for (int value : data) {
    bins[digit(value , 0)].push_back (value);
}
bins

{ { 30 }, { 91 }, { 92, 22 }, {}, {}, { 85, 15, 35 }, { 6 }, {}, {}, { 39 } }

• 3). Walk through each bin
  • for each value in the current bin, copy it back.
  • important to start at the "smallest" bin, otherwise, it won't work
• 4). clear each bin after copying elements

{
    auto i = data.begin();
    for (auto & bin : bins) {
        i = std::copy (bin.begin(), bin.end(), i);
        bin.clear();
    }
}
data

{ 30, 91, 92, 22, 85, 15, 35, 6, 39 }

• 5). Repeat the process for the NEXT significant digit (the ten's digit)

for (int value : data) {
    bins[digit(value , 1)].push_back (value);
}
bins

{ { 6 }, { 15 }, { 22 }, { 30, 35, 39 }, {}, {}, {}, {}, { 85 }, { 91, 92 } }

• 6). And copy the elements back over from the bins

{
    auto i = data.begin();
    for (auto & bin : bins) {
        i = std::copy (bin.begin(), bin.end(), i);
        bin.clear();
    }
}
data

{ 6, 15, 22, 30, 35, 39, 85, 91, 92 }

Pseudocode:

# d is the upper limit on the number of digits for a number
def radix_sort (nums, d=8):
    # create 10 empty bins
    bins = list(list() for i in range(10))
    # start at the ones digit
    div = 1
    for digit in range(d):
        # split nums into appropriate bins
        for num in nums:
            bins[(num // div) % 10].append(num)
        # copy from bins back to nums
        i = 0
        for b in range(10):
            for n in bins[b]:
                nums[i] = n
                i += 1
            bins[b].clear()
        # update to "next" digit
        div *= 10

Complexity Analysis

• What is the algorithmic complexity?

for digit in range(d):
   ...
   for num in nums:
      ...
   for b in range(10):
       for n in bins[b]:
          ...

• d and N
• What if d << N (d substantially smaller than N)

Counting Sort

Radix Sort seemed nice -- but what if we had a bunch of duplicate values?

• "Count" unique values (which can be used as indices)
• Take the counts and map them to destination indices
• copy all values over to the output vector
• copy everything back to the original input

Pseudocode (from Wikipedia)

function countingSort(array, k) is
  count ← new array of k zeros
  for i = 1 to length(array) do
    count[array[i]] ← count[array[i]] + 1
  for i = 2 to k do
    count[i] ← count[i] + count[i - 1]
  for i = length(array) downto 1 do
    output[count[array[i]]] ← array[i]
    count[array[i]] ← count[array[i]] - 1
  return output

Determining k

Given any set of numbers:

1. compute the min and max values
2. Range of elements is [min, max]
3. Size of range is max - min + 1
4. To make array access zero-index based,
   • idx = value - min

Takeaways:

• k can be initialized to size
• For any access to an index, use value - min instead of value

Example

• 1). Declare array
• 2). Determine min/max
• 3). Calculate $k$

#include <algorithm>
#include <numeric>

constexpr int N = 10;
int A[N] = {4, 1, 2, 3, 4, 3, 1, 2, 0, 4};

// int [min, max] = *std::minmax_element(A, A + N);
constexpr int min = 0, max = 4;
constexpr int k = max - min + 1;

A

{ 4, 1, 2, 3, 4, 3, 1, 2, 0, 4 }

• 4). create counting array (vector)
• 5). fill with zero
• 6). foreach value in input, increment count at correct index

int C[k]; // counting array
std::fill_n(C, k, 0);
for (int value : A) {
    ++C[value - min];
}
C

{ 1, 2, 2, 2, 3 }

• 7). Once we have our counts, convert them to a positional index
  • We leverage partial sums to do this

// convert counts to index (via partial_sum)
std::partial_sum(C, C + k, C);
C

{ 1, 3, 5, 7, 10 }

• 8). Create output vector of appropriate size
• 9). reverse iterate through inputs
  • Note: reversed because of partial sum
  • copy value from input array to output location
  • decrement index for destination

int B[N]; // output
for (int i = N - 1; i >= 0; --i) {
    B[--C[A[i] - min]] = A[i];
}
B

{ 0, 1, 1, 2, 2, 3, 3, 4, 4, 4 }

• 10). Copy all values from output back to input range

std::copy_n (B, N, A);
A

{ 0, 1, 1, 2, 2, 3, 3, 4, 4, 4 }