Intro to Algorithms + std::vector

CSCI 362: Data Structures

Prof. William Killian

Sorting

Three elementary sorting algorithms:

• Bubble
• Insertion
• Selection

Bubble Sort

#include <utility> // for std::swap

void bubble_sort (int* A, size_t N) {
    for (size_t i = N - 1; i >= 1; --i) {
        for (size_t j = 0; j < i; ++j) {
            if (A[j] > A[j + 1]) {
                std::swap (A[j], A[j + 1]);
            }
        }
    }
}

• Complexity?
• What are we counting? What is the worst case?

int a[10] = {9, 2, 10, 3, 1, 8, 4, 7, 5, 6};
bubble_sort (a, 10);
a

{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }

Optimized(?) Bubble Sort

void bubble_sort_opt (int* A, size_t N) {
    for (size_t i = N - 1; i >= 1; --i) {
        bool didSwap = false;
        for (size_t j = 0; j < i; ++j) {
            if (A[j] > A[j + 1]) {
                std::swap (A[j], A[j + 1]);
                didSwap = true;
            }
        }
        if (!didSwap) {
            break;
        }
    }
}

int b[10] = {9, 2, 10, 3, 1, 8, 4, 7, 5, 6};
bubble_sort_opt (b, 10);
b

{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }

Insertion Sort

void insertion_sort (int* A, size_t N) {
    for (size_t i = 1; i < N; ++i) {
        // Invariant: A[0..i) is sorted
        int v = A[i]; // element to place
        int j = i;    // Index to place 'v'
        while (j >= 1 && v < A[j - 1]) {
            A[j] = A[j - 1];
            --j;
        }
        // Invariant: j == 0 or v >= A[j - 1]
        A[j] = v;
    }
}

int c[10] = {9, 2, 10, 3, 1, 8, 4, 7, 5, 6};
insertion_sort (c, 10);
c

{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }

Selection Sort

void selection_sort (int* A, size_t N) {
    // Find smallest and place. Repeat
    for (size_t i = 0; i < N - 1; ++i) {
        size_t min = i;
        for (size_t j = i + 1; j < N; ++j) {
            if (A[j] < A[min]) {
                min = j;
            }
        }
        /* if (i != min) */ {
            std::swap (A[i], A[min]);
        }
    }
}

int d[10] = {9, 2, 10, 3, 1, 8, 4, 7, 5, 6};
selection_sort (d, 10);
d

{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }

Searching

• Sequential: examine $0^{th}$ element, then $1^{st}$, and so on...

std::find() in <algorithm> header

#include <iostream>
#include <algorithm>
int e[10] = {1, 10, 3, 8, 2, 4, 9, 5, 7, 6};

int val = 13;
int* pos = std::find (e, e + 10, val);
if (pos != e + 10) {
    std::cout << *pos;
} else {
    std::cout << "not found :(";
}

not found :(

More Searching

Binary Search

• Requires the sequence to be sorted
• More efficient!

d

{ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 }

pos = std::lower_bound (d, d + 10, 13);
// *pos >= val or pos @ end
std::distance(d, pos)

10

std::binary_search (d, d + 10, 2)

true

Binary Search

1. If the array is empty, return not found (Case 0)
2. Look at the middle element
   • If match, return location (Case 1)
   • If target smaller, search left sub-array (Case 2)
   • If target larger, search right sub-array (Case 3)

Range Notation:

• Array A has valid indicies in the range of 0 (inclusive) to N (exclusive)

  A[0..N)

• Range notation is useful when we want to SPLIT or JOIN ranges:

  A[0..N) <=> A[0..m) A[m..N)

Case 0: Not Found

if (first >= last) {
  return -1;
}

Case 1: Match

if (target == midValue) {
  return mid;
}

Case 2: Target smaller than middle value

if (target < midValue) {
  /* reposition last to mid */
  /* search subarray A[first .. mid) */
}

Case 3: Target larger than middle value

if (target > midValue) {
  /* reposition first to mid + 1 */
  /* search subarray A[mid + 1 .. last) */
}

Example: Successful Binary Search

  0   1   2   3   4   5   6   7   8   9
+---+---+---+---+---+---+---+---+---+
|-7 | 3 | 5 | 8 | 12| 16| 23| 33| 55|
+---+---+---+---+---+---+---+---+---+
^               ^                   ^
lo             mid                  hi

target: 23 lo: 0 hi: 9

mid: halfway between first and last = 4

(target = 23) > (midvalue = 12) --- Case 3

  0   1   2   3   4   5   6   7   8   9
+---+---+---+---+---+---+---+---+---+
|-7 | 3 | 5 | 8 | 12| 16| 23| 33| 55|
+---+---+---+---+---+---+---+---+---+
                    ^       ^       ^
                    lo     mid      hi

target: 23 lo: 5 hi: 9

mid: halfway between first and last = 7

(target = 23) < (midvalue = 33) --- Case 2

  0   1   2   3   4   5   6   7   8   9
+---+---+---+---+---+---+---+---+---+
|-7 | 3 | 5 | 8 | 12| 16| 23| 33| 55|
+---+---+---+---+---+---+---+---+---+
                    ^   ^   ^
                    lo mid  hi

target: 23 lo: 5 hi: 7

mid: halfway between first and last = 6

(target = 23) == (midvalue = 23) --- Case 1

Example: Unsuccessful Binary Search

  0   1   2   3   4   5   6   7   8   9
+---+---+---+---+---+---+---+---+---+
|-7 | 3 | 5 | 8 | 12| 16| 23| 33| 55|
+---+---+---+---+---+---+---+---+---+
^               ^                   ^
lo             mid                  hi

target: 4 lo: 0 hi: 9

mid: halfway between first and last = 4

(target = 4) < (midvalue = 12) --- Case 2

  0   1   2   3   4   5   6   7   8   9
+---+---+---+---+---+---+---+---+---+
|-7 | 3 | 5 | 8 | 12| 16| 23| 33| 55|
+---+---+---+---+---+---+---+---+---+
^       ^       ^          
lo     mid      hi

target: 4 lo: 0 hi: 4

mid: halfway between first and last = 2

(target = 4) < (midvalue = 5) --- Case 2

  0   1   2   3   4   5   6   7   8   9
+---+---+---+---+---+---+---+---+---+
|-7 | 3 | 5 | 8 | 12| 16| 23| 33| 55|
+---+---+---+---+---+---+---+---+---+
^   ^   ^                 
lo mid  hi

target: 4 lo: 0 hi: 2

mid: halfway between first and last = 1

(target = 4) > (midvalue = 3) --- Case 3

  0   1   2   3   4   5   6   7   8   9
+---+---+---+---+---+---+---+---+---+
|-7 | 3 | 5 | 8 | 12| 16| 23| 33| 55|
+---+---+---+---+---+---+---+---+---+
        ^
        lo
        mid
        hi

target: 4 lo: 2 hi: 2

mid: halfway between first and last = 2

first >= last --- Case 0

size_t binary_search (int const * A, size_t N, int target) {
    size_t first = 0;
    size_t last = N;
    // Tests for a non-empty sublist
    while (first < last) {
        size_t mid = first + (last - first) / 2;
        if (target == A[mid]) {
            return mid;
        } else if (target < A[mid]) {
            last = mid;
        } else {
            first = mid + 1;
        }
    }
    return -1;
}

int f[9] = {-7, 3, 5, 8, 12, 16, 23, 33, 55};

binary_search (f, 9, 5)

2

(int)binary_search (f, 9, 34)

-1

binary_search (f, 9, 12)

4

binary_search (f, 9, -7)

0

Observations of Binary Search

$mid = first + \frac{last - first}{2}$

versus

$mid = \frac{first + last}{2}$

• When searching for "zyzzyva" would you start looking in the middle of the dictionary?

Interpolation Search

Knowing the upper and lower limits of a sorted range, we can:

1. Estimate the position of a "key"
2. Obtain better performance if the data is uniformly distributed
   • Phone book is somewhat uniform
   • [1, 10, 100, 1000, ...] would not be

Example:

• Array consisting of 1,000 elements
• First element is 1,000
• Last element is 1,000,000
• Search value is 12,000
• Question: Where should we first look?

Binary Search

$$mid = \frac{first + last}{2} = \frac{0 + 1,000}{2} = 500$$

Interpolation Search (note: $last$ is inclusive)

$$mid = \frac{val - A[first]}{A[last] - A[first]} \times (last - first)$$

 

$$mid = \frac{12,000 - 1,000}{1,000,000 - 1,000} \times (999 - 0) $$

 

$$ mid = \frac{11,000}{990,000} \times 999 = 11 $$

• Calculation is more costly than binary search
• Uses a more expensive division
• One iteration could be slower than complete binary search
• Question: how do you interpolate strings?
• Complexity (average): $O(lg(lg(N))) = O(lg^{(2)}N)$
  • Worst case: $O(N)$

size_t interpolation_search (int const * A, size_t N, int target) {
    size_t s = 0;
    size_t e = N - 1;
    if (target < A[s]) return -1;
    if (target >= A[e]) s = e;
    while (s < e) {
        size_t loc = s + (e - s) * (target - A[s]) / (A[e] - A[s]);
        if (target == A[loc]) {
            return loc;
        } else if (target < A[loc]) {
            e = loc - 1;
        } else {
            s = loc + 1;
        }
    }
    if (target == A[s]) {
        return s;
    }
    return -1;
}

Algorithm Complexity

• Big-O notation
  • Machine-independent means for expressing efficiency
• Count key operations and relate this count to problem size using
  1. growth function
  2. (or) runtime function
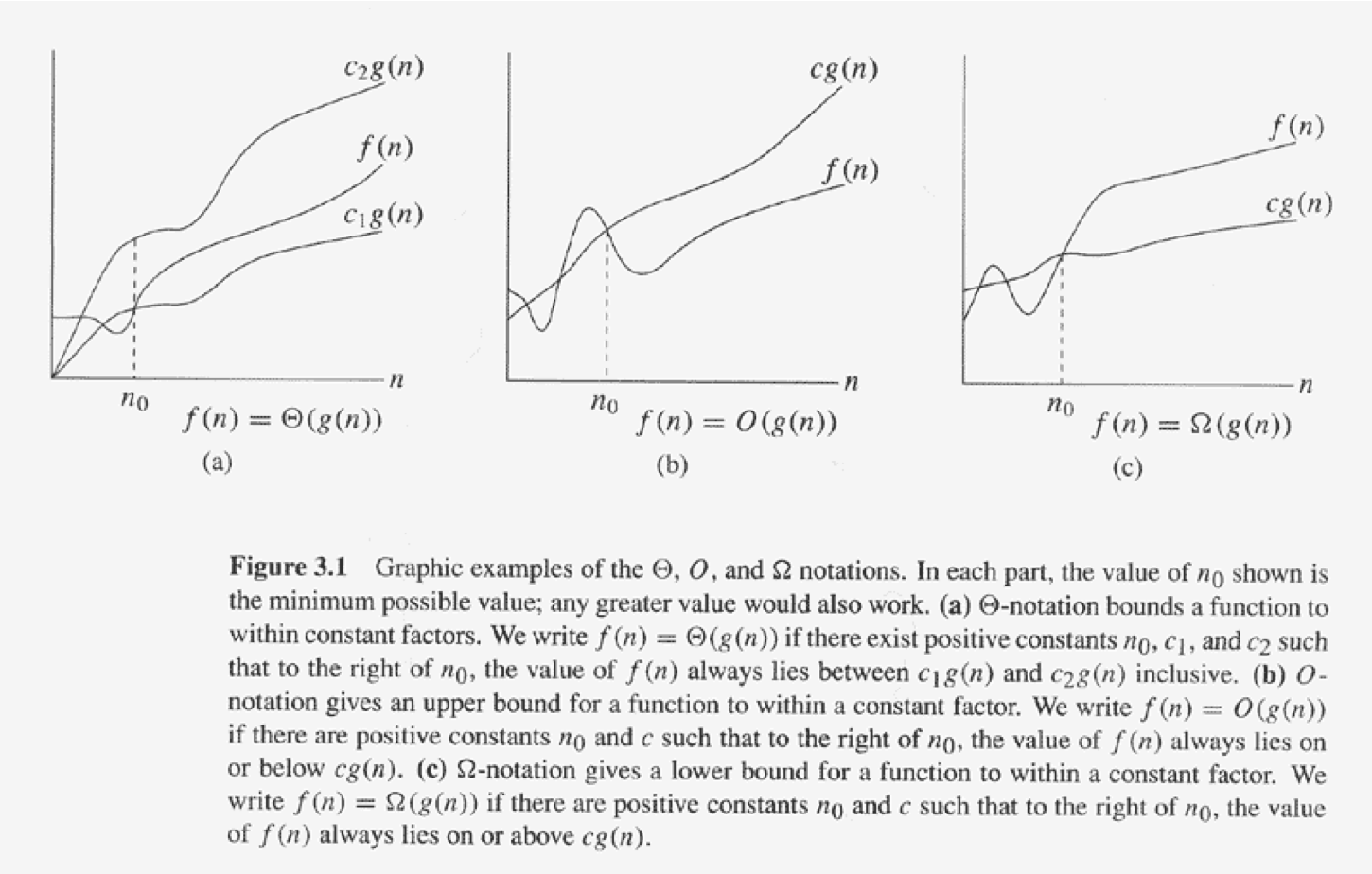
• $f(N) = O(g(N))$ if there exists positive constants $c$ and $n_0$ such that

$f(N) \le c * g(N)$ when $N \ge n_0$

Example growth (runtime) functions:

• $f_1(N) = 3N^2 + 50N + 120$
• $f_2(N) = 1000 * lg(N) + 50$
• $f_3(N) = 5$

Show $f_1(N) = O(N^2)$

Let $n_0 = 1$

$f_1(N) = 3N^2 + 50N + 120$

$f_1(N) \le 3N^2 + 50N^2 + 120N^2 = 173N^2$

Choose $c = 173$

Therefore $f_1(N) \le 173N^2 \Rightarrow O(N^2)$

Show $f_3(N) = O(1)$

Let $n_0 = 1, c = 6$

$f_3(N) = 5 \le 6 * 1)$

Constant Time Algorithms

An algorithm is $O(1)$ (constant time) when its complexity is independent of input size

Example:

std::vector<T>::push_back(T const& value);

• When capacity() > size(), push_back() has $O(1)$ complexity

Linear Time Algorithms

An algorithm is $O(N)$ (linear time) when its runtime is proportional to input size

Example:

Sequential search for minimum element in an array

Iterator std::min_element (Iterator begin, Iterator end, Value const& v);

• No matter how many elements are in the array, we must check the value of each element

Polynomial Algorithms

Algorithms with running time $O(N^2)$ are quadratic

• Practical only for relatively small values of $N$. Examples?
• Tripling $N$ increases the runtime by ?

Algorithms with running time $O(N^3)$ are cubic

• Efficiency is generally poor. Examples?
• Tripling $N$ increases the runtime by ?

Algorithm Complexity Chart

     n   lg(n)       n*lg(n)           n^2           n^3           2^n
     2       1             2             4             8             4
     4       2             8            16            64            16
     8       3            24            64           512           256
    16       4            64           256          4096         65536
    32       5           160          1024         32768   4.29497e+09
   128       7           896         16384   2.09715e+06   3.40282e+38
  1024      10         10240   1.04858e+06   1.07374e+09  1.79769e+308
 65536      16   1.04858e+06   4.29497e+09   2.81475e+14           inf

Function Templates

A function's logic could be appropriate for different types

• We want to make the function generic
• "Templatize" the function
• Useful for sorting, searching and other algorithms
• Useful for collection operations: insert, erase, find...
• Similar to Java? ... sort of

Selection Sort Algorithm (for ints)

void selection_sort (int* A, size_t N) {
  ...
  int temp;
  for (size_t i = 0; i < N - 1; ++i) {
    ...
      if (A[j] < A[min]) {
        ...
      }
    ...
  }
}

Selection Sort Algorithm (for std::strings)

void selection_sort (std::string* A, size_t N) {
  ...
  std::string temp;
  for (size_t i = 0; i < N - 1; ++i) {
    ...
      if (A[j] < A[min]) {
        ...
      }
    ...
  }
}

Selection Sort Algorithm (for generic type Ts)

template <typename T>
void selection_sort (T* A, size_t N) {
  ...
  T temp;
  for (size_t i = 0; i < N - 1; ++i) {
    ...
      if (A[j] < A[min]) {
        ...
      }
    ...
  }
}

Key Insight: operator< MUST be defined for type T

Template Functions

template

• tells the compiler that we are writing something that is "templatized"

typename T

• tells the C++ compiler that T should be referred to as a type whenever it appears

NOTE: Always comes at the very beginning of any function or class definition

C++ Standard Library Containers

• C++ provides 16 container classes implementing ADTs with various data structures
• Container Categories
  • Sequence
    • array, vector, list, forward_list, deque
    • access elements based off their position -- $O(1)$ to $O(N)$
    • index starts at zero
  • Associative
    • (unordered_)(multi)set, (unordered_)(multi)map
    • access elements based off their key -- $O(1)$ to $O(lg(N))$
    • may bear no relationship to where it's stored
  • Adapters
    • stack, queue, priority_queue
    • use sequence container as underlying storage
    • Design Pattern: Adapter (Adapter's interface provides a restricted set of operations)

Adapters

Stack

A stack allows access only at one end of the sequence, called top

#include <stack>
std::stack<char> s;

You insert into a stack using push()

s.push('G');
s.push('C');
s.push('D');
s.size()

3

If you want to access the element at the top of the stack, use top()

s.top()

'D'

Calling top() doesn't change the stack! It returns a copy

s.top()

'D'

If you want to remove an element, use pop()

Problem: pop() doesn't return anything!

s.pop() // [G, C, D] -- removes the D

So if you want the value before pop() you must call top()

template <typename T, typename Container>
T pop(std::stack<T, Container>& s) {
  T value = s.top();
  s.pop();
  return value;
}

pop(s)

'C'

Queue

A queue allows insertion to the back and removal from the front

#include <queue>
std::queue<int> q

• access the element at the front of the queue, call front()
• access the element at the back of the queue, call back()
• access the size of the queue, call size()

You insert into a queue using push() (same as stack!)

q.push(3);
q.push(6);
q.push(2);

q.front()

3

q.back()

2

q.size()

3

If you want to remove an element, use pop()

Problem: pop() doesn't return anything!

template <typename T, typename Container>
T pop(std::queue<T, Container>& q) {
  T value = q.front();
  q.pop();
  return value;
}

pop(q)

3

pop(q)

6

Priority Queue

A priority queue has a highest priority, first out protocol

#include <queue>
std::priority_queue<int> pq;
pq.push(3);
pq.push(6);
pq.push(2);

pq.top()

6

pq.pop();
pq.top()

3

Associative Containers

Set

A set maintains a collection of unique values called keys

#include <set>
#include <initializer_list>

std::set<int> set = {3, 2, 1, 9, 1, 4};
set

{ 1, 2, 3, 4, 9 }

std::multiset<int> multiset = {3, 2, 1, 9, 1, 4};
multiset

{ 1, 1, 2, 3, 4, 9 }

Map

A map maintains a collection of key-value pairs

#include <map>
#include <string>
using namespace std::literals::string_literals;

std::map<int, std::string> students =
  { {12, "Bob"s}, {30, "Alice"s}, {4, "Charlie"s}};

students

{ 4 => "Charlie", 12 => "Bob", 30 => "Alice" }

Sequence Containers

C++ Arrays

• Fixed-size collection – homogenous
• Stores $N$ elements in contiguous block of memory

int arr[N]; // where N is a compile-time constant

Evaluating a C++ Array as a container

• Size is fixed at the time of its declaration
• Does an array know its size?
• Can you do this?

std::cin >> N;
int A[N];

• C++ arrays do not allow assignment of one array to another
• Requires loop with the array size as an upper bound
  • or std::copy algorithm

int N = 4;
int A[N];

input_line_84:3:5: error: variable length array declaration not allowed at file scope
int A[N];
    ^ ~

Interpreter Error: 

C++ array class

C++11 array is more flexible than plain array, but not as flexible as a vector

• Size is still fixed at time of its declaration
• Two template parameters: type and size

#include <array>
constexpr int N = 10;
std::array<int, N> arr;
arr.size()

10

arr.fill(1337);
arr[5]

1337

Vector

vector overcomes the limitations of array

• Dynamically resizable
• Know their length and capacity
• Elements still stored contiguously -- $O(1)$ element access
• Easily copied

std::vector API

Defined in header <vector>

namespace std {
  template <
    typename T,                            // value type to store
    typename Allocator = std::allocator<T> // how to allocate data
  > class vector;
}

#include <iostream>
#include <vector>

template <typename T>
std::vector<T>
printSizeAndCapacity (std::vector<T>&& v) {
    std::cout << "Size: " << v.size() << '\n';
    std::cout << "Capacity: " << v.capacity() << '\n';
    return v;
}

std::vector Special Member Datatypes

Name	Description
T	template parameter for value type to store
value_type	alias to T
size_type	unsigned integer type (usually std::size_t)
difference_type	signed integer type (usually std::ptrdiff_t)
reference	alias to value_type&
const_reference	alias to value_type const&
pointer	usually just value_type*
const_pointer	usually just value_type const*
iterator	aliased to value_type*
const_iterator	aliased to value_type const*
reverse_iterator	std::reverse_iterator<iterator>
const_reverse_iterator	std::reverse_iterator<const_iterator>

std::vector Contructors

vector ();
vector (size_type n);
vector (size_type n, T const& value);

template <typename InputIterator>
vector (InputIterator first, InputIterator last);

vector (std::initializer_list<T>);

vector()

• create an empty vector

printSizeAndCapacity(std::vector<int>{})

Size: 0
Capacity: 0

{}

vector(size_type n)

• create a vector with $n$ elements (default-constructed)

printSizeAndCapacity(std::vector<int>(5))

Size: 5
Capacity: 5

{ 0, 0, 0, 0, 0 }

vector(size_type n, T const& value)

• create a vector with $n$ elements initialized to value

printSizeAndCapacity(std::vector<int>(5, 2))

Size: 5
Capacity: 5

{ 2, 2, 2, 2, 2 }

template <typename InputIterator>
vector(InputIterator first, InputIterator last);

• initialize the vector using the range [first, last)
• first and last are input iterators -- we'll talk about them later

vector(std::initializer_list<T> list);

• initialize the vector using the initializer list

printSizeAndCapacity(std::vector<int>{5, 4, 3, 2, 1})

Size: 5
Capacity: 5

{ 5, 4, 3, 2, 1 }

std::vector Access Operations

reference back ();
      reference front ();
      reference operator[] (size_type i);  
      reference at (size_type i);
      pointer   data ()                         noexcept;

std::vector Access Operations (const versions)

const_reference back ()                  const;
const_reference front ()                 const;
const_reference operator[] (size_type i) const;  
const_reference at (size_type i)         const;
const_pointer   data ()                  const noexcept;

reference back ();

• return the value of the item at the rear (or back) of the vector
• Precondition: the vector must contain at least one element

 

const_reference back() const;

• const version of back()

[] () -> int& {
    static std::vector<int> a = {1, 2, 3};
    return a.back();
}()

3

[] () -> int const& {
    const static std::vector<int> a = {1, 2, 3};
    return a.back();
}()

3

reference operator[] (size_type i);

• Allows the vector element at index $i$ to be retrieved or modified
• Precondition: $0 \le i < n \mid n=$ size of the vector
• Postcondition: If the operator appears on the left side of an assignment statement, the expression on the right side modifies the element referenced by the index

 

reference at (size_type i);

• Behaves exactly like operator[] but does run-time bounds checking
• Throws an exception if the precondition isn't met

[] {
    std::vector<int> a = {1, 2, 3};
    return a[1];
}()

2

[] {
    std::vector<int> a = {1, 2, 3};
    return a.at(4);
}()

Standard Exception: vector::_M_range_check: __n (which is 4) >= this->size() (which is 3)

std::vector Capacity Operations

bool      empty ()                     const;
size_type size ()                      const;
size_type capacity ()                  const;
size_type max_size ()                  const;
void      shrink_to_fit ();
void      reserve (size_type newcap);

bool empty() const;

• returns true IFF the vector's size is zero

 

size_type size () const

• returns the current size of the vector

 

size_type capacity() const;

• returns the number of elements that the container has currently allocated space for.

void shrink_to_fit();

• Requests the removal of unused capacity by reducing capacity() to size()
• Postcondition: if reallocation occurs, all iterators and all references are invalidated

 

void reserve(size_type newcap);

• Increase the capacity of the vector to a value that is $\ge newcap$
• If $newcap$ > capacity() then new storage is allocated; otherwise, the method does nothing
• Postcondition: capacity() $\ge newcap$, size is unchanged

std::vector Iterator Operations

iterator               begin ()  noexcept;
iterator               end ()    noexcept;
reverse_iterator       rbegin () noexcept;
reverse_iterator       rend ()   noexcept;
const_iterator         begin ()  const noexcept; // and cbegin()
const_iterator         end ()    const noexcept; // and cend()
const_reverse_iterator rbegin () const noexcept; // and crbegin()
const_reverse_iterator rend ()   const noexcept; // and crend()

std::vector Modifying Operations

void     clear();

void     pop_back ();
iterator erase (...);  // 2 versions

iterator insert (...); // 5 versions
void     push_back (const_reference value); // and "move" variant

template <typename ... Args>
iterator emplace (const_iterator pos, Args&& ... value);

template <typename ... Args>
void     emplace_back (Args&& ... value);

void     resize(...);  // 2 versions

void push_back (const_reference value);

• Adds a value at the rear of the vector
• Postcondition: The vector has a new element at the rear; size is increased by 1

 

void pop_back ();

• Removes a value from the rear of the vector
• Precondition: The vector is not empty
• Postcondition: The vector's last element has been removed or is empty; size decreases by 1

iterator insert (const_iterator pos, const_reference value);

• inserts $value$ before $pos$ and returns an iterator pointing to the position of the new value in the vector
• NOTE: this operation may invalidate any existing iterators if the capacity needs increased
• Postcondition: The vector has a new element; size is increased by 1

 

iterator erase (const_iterator pos);

• Erase the element pointed to by $pos$
• NOTE: all iterators beyond the elements erased are invalidated
• Precondition: The vector is not empty
• Postcondition: The vector has one less element; size is decreased by 1

iterator erase (const_iterator first, const_iterator last);

• Erases the range of all elements in [first, last)
• NOTE: all iterators beyond the elements erased are invalidated
• Precondition: The vector is not empty
• Postcondition: Size decreases by std::distance(first, last); the same number of elements are removed

 

void resize(size_type n);

• Modify the size of the vector. If the size is increased, the default value T() is filled for the increase in elements at the end. If the size is decreased, the original values at the front are retained.
• Postcondition: The vector has size $n$

Using std::vector

• Outputting vectors
  • for-loop
  • range-based for-loop
• Using vector objects
  • sequenced operations
  • push_back vs. operator[]

Reminder: template-functions

template <typename T>
void insertionSort (std::vector<T>& v) {
    // Logic exactly the same as array version
    // ...
    //    while (j >= 1 && temp < v[j - 1])
    // ...
}

/New/: Class Templates

• Allows us to "templatize" classes as well as functions

• All container classes in C++ standard library are templates

• Syntax:

template <typename T1, typename T2, ...>
class ClassName
{
   ...
};

• Example:

template <typename T> class Store;

template <typename T>
class Store {
public:
    Store (const T& item = T())
    : m_value (item) { }
    
    T getValue() const {
        return m_value;
    }
    
    void setValue(const T& item) {
        m_value = item;
    }
    
private:
    T m_value;
};

// Using the class:

Store<double> s;
s.setValue(4.3);
s.getValue()

4.3

Store<int> s2 (10);
s2.getValue()

10