CSCI 162 - Lecture 12 - Chapter 9: Trees

Instructor's Class Notes

Introduction to Trees - A tree is a nonlinear data structure for storing information. It is unlike a linked list or an array that store data linearly with one data component followed by the next, and that followed by the next, etc. For the non-linear tree structure there is a more complex linking between data components. The nonlinear structure of of the storage often allows for significantly improved efficiencies in data access and updates.

It all starts with the root:

Note: In computer science the a tree is upside dowin in that it starts at the root and extends down to its branches.

Binary Tree - A binary tree is a finite set of nodes. The set might be empty (no nodes, which is called the empty tree). But if the set is not empty, it follows these rules:

There is one special node, called the root.
Each node can be associated with up to two other different nodes, called its left child and its right child. If a node c is the child of another node p, then we say that "p is c's parent."
Each node, except the root, has exactly one parent; the root has no parent.
If you start at a node and move to the node's parent (provided there is one), and then move again to that node's parent, and keep moving upward to each node's parent, you will eventually reach the root.

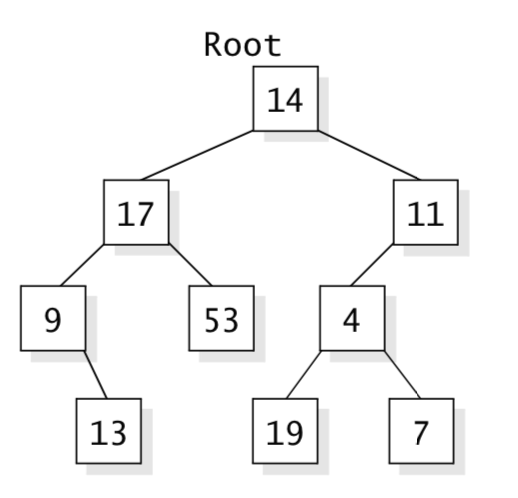
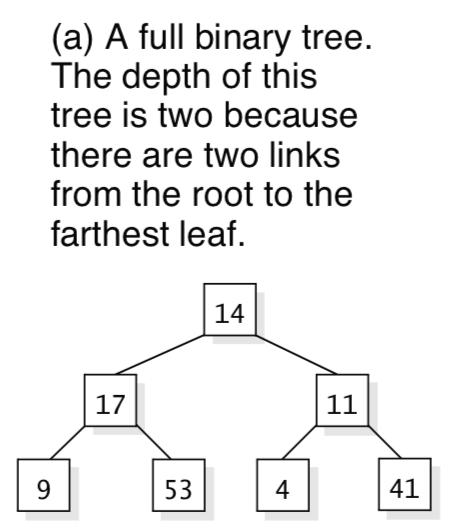
Examples of Binary Trees - Following are a few examples of binary trees:

Tree Terminology - Following are several terms related to trees:

Parent - The parent of a node is the node linked above it. More precisely, if a node c is the child of another node p, then we say that "p is c's parent.: Except for the root, every node has just one parent, and the root has no parent. In Figure (a) above, the node containing 17 is the parent of the nodes containing 9 and 53.
Sibling - Two nodes are siblings if they have the same parent. In Figure (a) above, the nodes containing 9 and 53 are siblings.
Ancestor - A node's parent is its first ancestor. The parent of the parent is the next ancestor. The parent of the parent of the parent is the next ancestor ... and so forth, until you reach the root. The root is an ancestor of each other node.
Descendant - A node's children are its first descendants. The children's children are its next descendants. The children of the children of the children are ... well, you get the idea.
Subtree - Any node in a tree also can be viewed as the root of a new, smaller tree. This smaller tree contains the node we've picked as the new root and all of the new root's descendants. This is called a subtree of the original tree. In Figure (a) above, we may choose 17 as the root of a new subtree, and that subtree has three nodes: the nodes containing 17, 9, and 53.
Left and Right Subtrees of a Node - For a node in a binary tree, the nodes beginning with its left child and below are its left subtree. The nodes beginning with its right child and below are its right subtree.
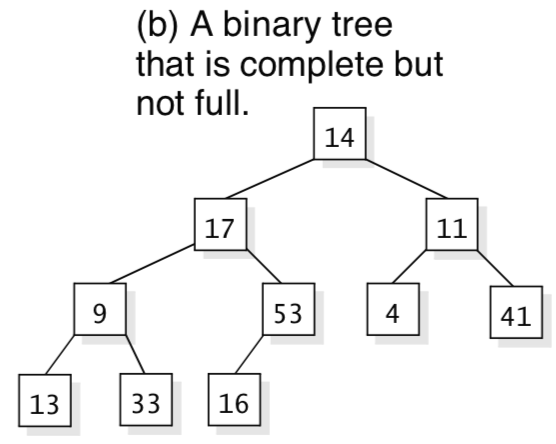
Depth of a Node - Suppose you start at a node n and move upward to its parent. We'll call this "one step." Then move up to the parent of the parent - that's a second step. Eventually, you will reach the root, and the number of steps taken is called the depth of the node n. The depth of the root itself is zero; a child of the root has depth one. In Figure (b) above, the node containing 13 has depth three.
Depth of a Tree - The depth of a tree is the maximum depth of any of its leaves. In Figure (b) above, the leaf containing 13 has depth three, and there is no deeper leaf. So the depth of the example tree is three. If a tree has only one node, the root, then its depth is zero (since the depth of the root is zero). The empty tree doesn't have any leaves, so we use -1 for its depth. Just to confuse things, you'll often see the term height used instead of depth, but they both mean the same thing.
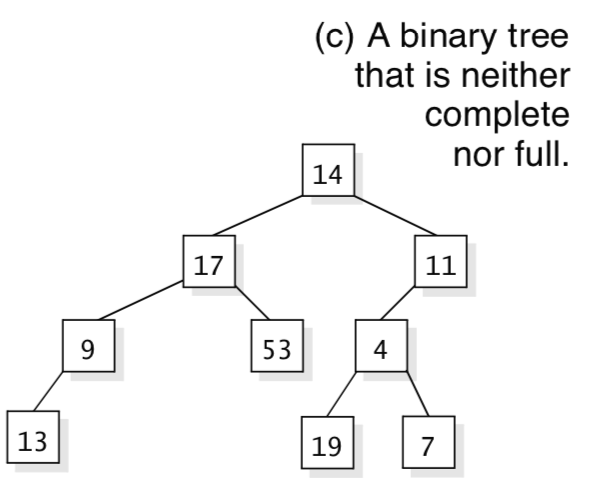
Full Binary Trees - In a full binary tree, every leaf has the same depth, and every non-leaf has two children. The first figure above with root of 14 is not a full tree, because it has leaves at different depths - some with depth two and some with depth three. Also, some of the non-leaves have only one child. In Figure (a) above is full, but figures (b) and (c) above are not full.
Complete Binary Trees - Suppose you take a full binary tree and start adding new leaves at a new depth from left to right. All the new leaves have the same depth - one more than where we started and we always add leftmost nodes first. For example, if you add three nodes to Figure (a) above, then one possible result is Figure (b) above. The tree is no longer a full tree because some leaves are a bit deeper than others. Instead, we call this a complete binary tree. To be a complete tree, every level except the deepest must contain as many nodes as possible; and at the deepest level, all the nodes are as far left as possible. In run- time analysis, it's important to know that a complete binary tree of depth n has the maximum number of leaves for that depth (2n) and the maximum number of total nodes (2n+1 - 1).

General Tree - Like a binary tree but each node can have several (zero, 1 or more) child nodes (not just 1 or 2).

BTNode - A generic Binary Tree class

Documentation: http://www.cs.colorado.edu/~main/docs/edu/colorado/nodes/BTNode.html
Source: http://www.cs.colorado.edu/~main/edu/colorado/nodes/BTNode.java

Binary Tree Traversal - The process of using a tree structure to process all of the nodes in a tree, applying the same operation to each node. There are three types of traversals:

pre-order traversal - The word "pre-order" refers to when the root is processed; it is processed previous to its two subtrees. So a pre-order traversal has these three steps for a non-empty tree:
1. Process the root.
2. Process the nodes in the left subtree with a recursive call.
3. Process the nodes in the right subtree with a recursive call.
```
public void preorderPrint( ) {
	System.out.println(data);
	if (left != null)
		left.preorderPrint( );
	if (right != null)
		right.preorderPrint( );
}
```
Example:

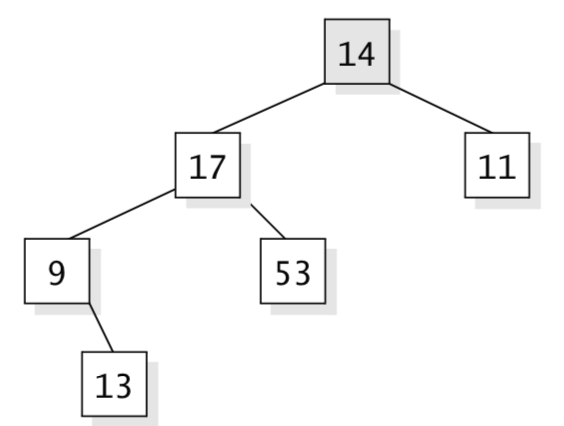
Output:
```
	14
	17
	9
	13
	53
	11				
					
```
in-order traversal - For "in-order" traversal the main difference iis that the root is processed in between the processing of its two subtrees. Here are the three steps for a non-empty tree:
1. Process the nodes in the left subtree with a recursive call.
2. Process the root.
3. Process the nodes in the right subtree with a recursive call.
```
public void inorderPrint( ) {
	if (left != null
		left.inorderPrint( );
	System.out.println(data);
	if (right != null)
		right.inorderPrint( );
}
```
Example:

Output:
```
	9
	13
	17
	53
	14
	11
					
```
post-order traversal - In "post-order" traversal the processing of the root is postponed until last in a non-empty tree (think of it as bottom up, left to right):
1. Process the nodes in the left subtree with a recursive call.
2. Process the nodes in the right subtree with a recursive call.
3. Process the root.
```
public void postorderPrint( ) {
	if (left != null
		left.postorderPrint( );
	if (right != null)
		right.postorderPrint( );
	System.out.println(data);	
}
```
Example:

Output:
```
	13
	9
	53
	17
	11
	14
					
```